Les maths pour le concours IFSI.
Modérateurs : Modérateurs, Concours IFSI
Suites
Bonjour,
Je passe le concours infirmier cette année et je rencontre de grosses difficultés avec les suites.
Surtout celles-ci :
- 34 204 1020 4080 12240
- 10 5 12 7 2
- 7 14 56 336 2688 26880
Si quelqu'un peut m'éclairer précisément s'il vous plait.
Cordialement.
LAXENAIRE Emily
Je passe le concours infirmier cette année et je rencontre de grosses difficultés avec les suites.
Surtout celles-ci :
- 34 204 1020 4080 12240
- 10 5 12 7 2
- 7 14 56 336 2688 26880
Si quelqu'un peut m'éclairer précisément s'il vous plait.
Cordialement.
LAXENAIRE Emily
Montpellier As : 18, 60 ème sur liste d'attente.
Aurillac : 6 en culture générale 10 en maths !
Nîmes via l'armée : Pas admis ! pas encore les notes !
Rodez : 18 en culture générale ! 7 en maths !
Aurillac : 6 en culture générale 10 en maths !
Nîmes via l'armée : Pas admis ! pas encore les notes !
Rodez : 18 en culture générale ! 7 en maths !
Re: Suites
Hé hé !!! 
Pour le premier c'est : multiplier par 6, puis par 5, par 4, par 3, par 2 (soit 24480)
Pour le deuxième peut-être :
Tu retires 3 de 10 qui fait 7
Tu retires 3 de 5 qui fait 2
Tu retires 3 de 12 qui fait 9
ça parait un peu tordu mais j'ai pas mieux !
Voilà Rattata
Pour le troisième : multiplier par 2, puis 4, puis 6, puis 8, puis 10, puis 12 (soit 322560)
Anerick du blog "Péripéties d'une infirmière"
Pour le premier c'est : multiplier par 6, puis par 5, par 4, par 3, par 2 (soit 24480)
Pour le deuxième peut-être :
Tu retires 3 de 10 qui fait 7
Tu retires 3 de 5 qui fait 2
Tu retires 3 de 12 qui fait 9
ça parait un peu tordu mais j'ai pas mieux !
Voilà Rattata
Pour le troisième : multiplier par 2, puis 4, puis 6, puis 8, puis 10, puis 12 (soit 322560)
Anerick du blog "Péripéties d'une infirmière"
Re: Suites
Ah d'accord, en fait la raison de la suite varie souvent !
Merci beaucoup !
Merci beaucoup !
Montpellier As : 18, 60 ème sur liste d'attente.
Aurillac : 6 en culture générale 10 en maths !
Nîmes via l'armée : Pas admis ! pas encore les notes !
Rodez : 18 en culture générale ! 7 en maths !
Aurillac : 6 en culture générale 10 en maths !
Nîmes via l'armée : Pas admis ! pas encore les notes !
Rodez : 18 en culture générale ! 7 en maths !
- supercuisto
- Accro

- Messages : 1120
- Inscription : 05 mars 2012 20:37
Re: Mathématiques concours 2013
Les problèmes de temps et vitesse
Ce sont les problèmes où l’on vous demande de calculer des vitesses, des distances parcourues, des temps nécessaire pour parcourir ces distances et même pire, des heures et des lieux de rencontre d’objets se déplaçant !
Pour résoudre ce type de problème, il n’y a qu’une formule simple et quelques petites astuces à connaître. Il est également très important de faire attention aux conversions des unités de longueur et de temps.
Règle 1
La vitesse (v) d’un objet est égale à la distance (d) divisée par le temps (t) :
v = d / t
A noter que si la distance est en kilomètres et le temps en heures, la vitesse sera exprimée en km/h ; si la distance est en mètres, et le temps en secondes, la vitesse sera en m/s……
Exemple :
Une voiture a parcouru 140 km en 2 heures. Quelle est sa vitesse ?
V = 140 / 2 = 70 km/h
Règle 2
Un objet parcourant une distance (d) à une vitesse (v) mettra un temps (t) égal au quotient de la distance par la vitesse :
t = d / v
La distance et la vitesse doivent être exprimées grâce à la même mesure de longueur : si la distance est en km, la vitesse doit être en km/h, ou km/s….
Exemple :
Une voiture qui roule à 70 km/h mettra combien de temps à parcourir 140 km ?
t = 140/70 = 2 heures !
Règle 3
Un objet se déplaçant pendant un temps (t) à une vitesse (v) parcourra une distance (d) égale au produit de la vitesse par le temps :
d = v x t
La vitesse et le temps doivent être exprimés grâce à la même mesure de temps : si la vitesse est exprimée en km/h par exemple, le temps doit être exprimé en heure.
Exemple :
Quelle distance une voiture roulant à 70 km parcourra-t-elle en 2 heures ?
d = 70 x 2 = 140 km
ATTENTION
La vitesse moyenne n’est pas égale à la moyenne des vitesses !
Ces calculs sont souvent utilisés pour déterminer les lieux et moments des points de rencontre d’objets se déplaçant sur un même trajet. Il existe pour cela 2 méthodes simples et infaillibles.
Règle 4
Je veux trouver le point de rencontre d’objet se déplaçant l’un vers l’autre.
Si les vitesses des objets sont v et V (dans la même unité), ils se rapprochent l’un de l’autre à une vitesse égale à la somme de leur vitesse : v + V.
Si la distance les séparant est d, ils se croiseront donc au bout d’un temps t tel que :
t = d / (v + V)
Attention, si les deux objets ne sont pas partis au même moment, je calcule la distance (d) séparant les deux objets au moment du départ du dernier.
Exemple :
Si deux personnes partent au même moment de deux endroits distants de 4 km et marchent l’un vers l’autre, l’une à 8 km/h et l’autre à 2 km/h, quand et où se rencontreront-elles ?
T = 4 / (8+2) = 4 / 10 = 0.4 heure (soit 24 minutes)
On sait qu’ils se rencontreront au bout de 24 minutes.
En 24 minutes, celui qui marche à 8 km/h aura parcouru 3.2 km. (d= v x t = 8 x 0.4=3.2)
Ils se rencontreront donc au bout de 24 minutes à 3.2 km de point de départ de la première personne.
Règle 5
Je veux trouver le moment où un objet se déplaçant vers un autre objet moins rapide va le doubler.
Si l’objet le plus lent se déplace à une vitesse (v) et le plus rapide à une vitesse (V) dans la même unité, le plus rapide se rapproche du plus lent à une vitesse égale à la différence entre leurs vitesses : V –v.
D’ils sont séparés par une distance (d), le plus rapide doublera le plus lent au bout d’un temps (t) égal à :
t = d / (V-v)
Attention, si les deux objets ne sont pas partis au même moment, je calcule la distance (d) séparant les deux objets au moment du départ du dernier.
Exemple :
Si deux personnes partent au même moment de deux endroits distants de 3 km et marchent l’une derrière l’autre, l’une à 7km/h et l’autre à 2 km/h, combien de temps après leur départ et à quelle distance de son point de d »part la première doublera-t-elle la seconde ?
t = 3 / (7-2) = 3/5 = 0.6 heures (soit 36 minutes)
La première doublera la deuxième au bout de 36 minutes.
La première doublera la seconde à une distance (d) de son point de départ telle que :
D = 0.6 x 7 = 4.2 km.
La première personne dépassera donc la seconde au bout de 4.2 km et 36 minutes.
Ce sont les problèmes où l’on vous demande de calculer des vitesses, des distances parcourues, des temps nécessaire pour parcourir ces distances et même pire, des heures et des lieux de rencontre d’objets se déplaçant !
Pour résoudre ce type de problème, il n’y a qu’une formule simple et quelques petites astuces à connaître. Il est également très important de faire attention aux conversions des unités de longueur et de temps.
Règle 1
La vitesse (v) d’un objet est égale à la distance (d) divisée par le temps (t) :
v = d / t
A noter que si la distance est en kilomètres et le temps en heures, la vitesse sera exprimée en km/h ; si la distance est en mètres, et le temps en secondes, la vitesse sera en m/s……
Exemple :
Une voiture a parcouru 140 km en 2 heures. Quelle est sa vitesse ?
V = 140 / 2 = 70 km/h
Règle 2
Un objet parcourant une distance (d) à une vitesse (v) mettra un temps (t) égal au quotient de la distance par la vitesse :
t = d / v
La distance et la vitesse doivent être exprimées grâce à la même mesure de longueur : si la distance est en km, la vitesse doit être en km/h, ou km/s….
Exemple :
Une voiture qui roule à 70 km/h mettra combien de temps à parcourir 140 km ?
t = 140/70 = 2 heures !
Règle 3
Un objet se déplaçant pendant un temps (t) à une vitesse (v) parcourra une distance (d) égale au produit de la vitesse par le temps :
d = v x t
La vitesse et le temps doivent être exprimés grâce à la même mesure de temps : si la vitesse est exprimée en km/h par exemple, le temps doit être exprimé en heure.
Exemple :
Quelle distance une voiture roulant à 70 km parcourra-t-elle en 2 heures ?
d = 70 x 2 = 140 km
ATTENTION
La vitesse moyenne n’est pas égale à la moyenne des vitesses !
Ces calculs sont souvent utilisés pour déterminer les lieux et moments des points de rencontre d’objets se déplaçant sur un même trajet. Il existe pour cela 2 méthodes simples et infaillibles.
Règle 4
Je veux trouver le point de rencontre d’objet se déplaçant l’un vers l’autre.
Si les vitesses des objets sont v et V (dans la même unité), ils se rapprochent l’un de l’autre à une vitesse égale à la somme de leur vitesse : v + V.
Si la distance les séparant est d, ils se croiseront donc au bout d’un temps t tel que :
t = d / (v + V)
Attention, si les deux objets ne sont pas partis au même moment, je calcule la distance (d) séparant les deux objets au moment du départ du dernier.
Exemple :
Si deux personnes partent au même moment de deux endroits distants de 4 km et marchent l’un vers l’autre, l’une à 8 km/h et l’autre à 2 km/h, quand et où se rencontreront-elles ?
T = 4 / (8+2) = 4 / 10 = 0.4 heure (soit 24 minutes)
On sait qu’ils se rencontreront au bout de 24 minutes.
En 24 minutes, celui qui marche à 8 km/h aura parcouru 3.2 km. (d= v x t = 8 x 0.4=3.2)
Ils se rencontreront donc au bout de 24 minutes à 3.2 km de point de départ de la première personne.
Règle 5
Je veux trouver le moment où un objet se déplaçant vers un autre objet moins rapide va le doubler.
Si l’objet le plus lent se déplace à une vitesse (v) et le plus rapide à une vitesse (V) dans la même unité, le plus rapide se rapproche du plus lent à une vitesse égale à la différence entre leurs vitesses : V –v.
D’ils sont séparés par une distance (d), le plus rapide doublera le plus lent au bout d’un temps (t) égal à :
t = d / (V-v)
Attention, si les deux objets ne sont pas partis au même moment, je calcule la distance (d) séparant les deux objets au moment du départ du dernier.
Exemple :
Si deux personnes partent au même moment de deux endroits distants de 3 km et marchent l’une derrière l’autre, l’une à 7km/h et l’autre à 2 km/h, combien de temps après leur départ et à quelle distance de son point de d »part la première doublera-t-elle la seconde ?
t = 3 / (7-2) = 3/5 = 0.6 heures (soit 36 minutes)
La première doublera la deuxième au bout de 36 minutes.
La première doublera la seconde à une distance (d) de son point de départ telle que :
D = 0.6 x 7 = 4.2 km.
La première personne dépassera donc la seconde au bout de 4.2 km et 36 minutes.
ESI 2013 / 2016 a Tours CHRU
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
- supercuisto
- Accro

- Messages : 1120
- Inscription : 05 mars 2012 20:37
Re: Mathématiques concours 2013
Application problèmes de temps et distance.
Exercice 1 :
Quelle est la vitesse d’une voiture parcourant 1 690 km en 13 heures ?
Exercice 2 :
Quel est le temps mis par un oiseau volant à 60 km/h pour parcourir 20 km ?
Exercice 3 :
Quelle est la distance parcourue par un piéton marchant à 5 km/h pendant 15 minutes ?
Exercice 4 :
Si deux personnes partent au même moment de deux endroits distants de 3 km et marchent l’un vers l’autre, l’une à 7 km/h et l’autre à 5 km/h, combien de temps après leur départ et à quelle distance du point de départ de la première se croiseront-elles ?
Exercice 5 :
Si deux personnes partent au même moment de deux endroits distants de 1 km et marchent l’une derrière l’autre, l’une à 7 km/h et l’autre à 5 km/h, combien de temps après leur départ et à quelle distance de son point de départ la première doublera-t-elle la seconde ?
Exercice 1 :
Quelle est la vitesse d’une voiture parcourant 1 690 km en 13 heures ?
Exercice 2 :
Quel est le temps mis par un oiseau volant à 60 km/h pour parcourir 20 km ?
Exercice 3 :
Quelle est la distance parcourue par un piéton marchant à 5 km/h pendant 15 minutes ?
Exercice 4 :
Si deux personnes partent au même moment de deux endroits distants de 3 km et marchent l’un vers l’autre, l’une à 7 km/h et l’autre à 5 km/h, combien de temps après leur départ et à quelle distance du point de départ de la première se croiseront-elles ?
Exercice 5 :
Si deux personnes partent au même moment de deux endroits distants de 1 km et marchent l’une derrière l’autre, l’une à 7 km/h et l’autre à 5 km/h, combien de temps après leur départ et à quelle distance de son point de départ la première doublera-t-elle la seconde ?
ESI 2013 / 2016 a Tours CHRU
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
-
loovelygyal
- Messages : 15
- Inscription : 30 sept. 2012 10:04
Re: Mathématiques concours 2013
coucou je me joins à vous
1) 130 km/h
2) 20 km
3) 1.25 km
4) 0.6 km
5) en 21 minutes 42 scd et à la distance de 2.5 km
1) 130 km/h
2) 20 km
3) 1.25 km
4) 0.6 km
5) en 21 minutes 42 scd et à la distance de 2.5 km
E.S.I 2013/2016
s1 : usld
s1 : usld
Re: Mathématiques concours 2013
Lovely, je vais faire le méchant de service, mais c'est le truc con qui coute vachement de point, surtout qu'en IFSI les unités sont très demandées :
Si tu réponds 20 km à une question ou on te demande un temps, tu es sure d'avoir faux, même si le chiffre ou le calcul est bon.
Il faut absolument se relire....
Si tu réponds 20 km à une question ou on te demande un temps, tu es sure d'avoir faux, même si le chiffre ou le calcul est bon.
Il faut absolument se relire....
D'autres sauront mieux que moi et me corrigeront si besoin
-
loovelygyal
- Messages : 15
- Inscription : 30 sept. 2012 10:04
Re: Mathématiques concours 2013
HA OUI pufff j'ai pas fait attention nico 
2) 20 minutes
4) 15 minutes au bout 1.75 km
5) 30 minutes au bout 2.5 km
voilou
2) 20 minutes
4) 15 minutes au bout 1.75 km
5) 30 minutes au bout 2.5 km
voilou
E.S.I 2013/2016
s1 : usld
s1 : usld
Re: Mathématiques concours 2013
c'est le truc bête, mais j'ai eu des formateurs qui nous faisaient jongler entre G/L, G/DL, mmol/L, et dès que tu fais pas gaffe, hop, des points en moins.
Mais en finalité, comme des labos utilisent des unités et d'autres des différentes, ils n'avaient pas nécessairement tort ( Rien qu'a voir les gazs du sang qui peuvent se rendre en mmHg, ou en Kilopascal qui est véritablement l'unité internationale).
Mais en finalité, comme des labos utilisent des unités et d'autres des différentes, ils n'avaient pas nécessairement tort ( Rien qu'a voir les gazs du sang qui peuvent se rendre en mmHg, ou en Kilopascal qui est véritablement l'unité internationale).
D'autres sauront mieux que moi et me corrigeront si besoin
Re: Mathématiques concours 2013
Bonjour, voici mes réponses
1) 130 Km/h
2) 19,8 = 20 minutes
3) 1,25 Km
4) 15 minutes puis 1,75 km
5) 30 minutes puis 3,5 km
Je suis contente de pouvoir travailler avec vous
1) 130 Km/h
2) 19,8 = 20 minutes
3) 1,25 Km
4) 15 minutes puis 1,75 km
5) 30 minutes puis 3,5 km
Je suis contente de pouvoir travailler avec vous
- supercuisto
- Accro

- Messages : 1120
- Inscription : 05 mars 2012 20:37
Re: Mathématiques concours 2013
Désolée, j'avais oublié de poster la correction ! 
Vous n'êtes pas obligé de donner vos réponses ! Pour le moment j'essaye d'expliquer pour que tout le monde comprenne bien les maths ! (notament pour ceux et celles qui ont des lacunes à rattraper) ! Donc ce qui compte c'est pas tant les résultats mais plutot le déroulement des calculs, la logique de réponses ! Une fois toutes les leçons abordées on pourra sentrainer tous ensemble !
Exercice 1 :
Quelle est la vitesse d’une voiture parcourant 1 690 km en 13 heures ?
Règle 1 : v = d / t
v = 1690 / 13 = 130 km/h
Exercice 2 :
Quel est le temps mis par un oiseau volant à 60 km/h pour parcourir 20 km ?
Règle 2 : t = d /v
t = 20 /6 = 1/3 h = 20 minutes
Exercice 3 :
Quelle est la distance parcourue par un piéton marchant à 5 km/h pendant 15 minutes ?
Règle 3 : d = v x t
v et t doivent être exprimés à partir de la même unité de temps !
v = 5 km/h
t = 15 min = 15/60 h = 0.25 h
d = 5 x 0.25 = 1.25 km
Exercice 4 :
Si deux personnes partent au même moment de deux endroits distants de 3 km et marchent l’un vers l’autre, l’une à 7 km/h et l’autre à 5 km/h, combien de temps après leur départ et à quelle distance du point de départ de la première se croiseront-elles ?
D'après la règle 4, les deux personnes se rapprochent l'une de l'autre à une vitesse de 7 + 15 = 12 km/h.
Elles sont séparées de 3 km. Elles se croiseront donc au bout d'un temps t = 3 /12 = 1/4 h = 15 minutes (règle 2)
Elles se croiseront à une distance d du point de départ de la première telle que : d = 1/4 x 7 = 1.75 km (règle 3)
Exercice 5 :
Si deux personnes partent au même moment de deux endroits distants de 1 km et marchent l’une derrière l’autre, l’une à 7 km/h et l’autre à 5 km/h, combien de temps après leur départ et à quelle distance de son point de départ la première doublera-t-elle la seconde ?
Les deux personnes se rapprochent l'une de l'autre à une vitesse de 7 - 5 = 2 km/h (règle 5).
Elles sont séparées par une distance de 1 km. La première doublera donc la seconde au bout d'un temps t = 1/2 h = 30 minutes (règle 2)
La première doublera la seconde à une distance d de son point de départ telle que d = 1/2 x 7 = 3.5 km (règle 3)
Vous n'êtes pas obligé de donner vos réponses ! Pour le moment j'essaye d'expliquer pour que tout le monde comprenne bien les maths ! (notament pour ceux et celles qui ont des lacunes à rattraper) ! Donc ce qui compte c'est pas tant les résultats mais plutot le déroulement des calculs, la logique de réponses ! Une fois toutes les leçons abordées on pourra sentrainer tous ensemble !
Exercice 1 :
Quelle est la vitesse d’une voiture parcourant 1 690 km en 13 heures ?
Règle 1 : v = d / t
v = 1690 / 13 = 130 km/h
Exercice 2 :
Quel est le temps mis par un oiseau volant à 60 km/h pour parcourir 20 km ?
Règle 2 : t = d /v
t = 20 /6 = 1/3 h = 20 minutes
Exercice 3 :
Quelle est la distance parcourue par un piéton marchant à 5 km/h pendant 15 minutes ?
Règle 3 : d = v x t
v et t doivent être exprimés à partir de la même unité de temps !
v = 5 km/h
t = 15 min = 15/60 h = 0.25 h
d = 5 x 0.25 = 1.25 km
Exercice 4 :
Si deux personnes partent au même moment de deux endroits distants de 3 km et marchent l’un vers l’autre, l’une à 7 km/h et l’autre à 5 km/h, combien de temps après leur départ et à quelle distance du point de départ de la première se croiseront-elles ?
D'après la règle 4, les deux personnes se rapprochent l'une de l'autre à une vitesse de 7 + 15 = 12 km/h.
Elles sont séparées de 3 km. Elles se croiseront donc au bout d'un temps t = 3 /12 = 1/4 h = 15 minutes (règle 2)
Elles se croiseront à une distance d du point de départ de la première telle que : d = 1/4 x 7 = 1.75 km (règle 3)
Exercice 5 :
Si deux personnes partent au même moment de deux endroits distants de 1 km et marchent l’une derrière l’autre, l’une à 7 km/h et l’autre à 5 km/h, combien de temps après leur départ et à quelle distance de son point de départ la première doublera-t-elle la seconde ?
Les deux personnes se rapprochent l'une de l'autre à une vitesse de 7 - 5 = 2 km/h (règle 5).
Elles sont séparées par une distance de 1 km. La première doublera donc la seconde au bout d'un temps t = 1/2 h = 30 minutes (règle 2)
La première doublera la seconde à une distance d de son point de départ telle que d = 1/2 x 7 = 3.5 km (règle 3)
ESI 2013 / 2016 a Tours CHRU
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
- supercuisto
- Accro

- Messages : 1120
- Inscription : 05 mars 2012 20:37
Re: Mathématiques concours 2013
LES FRACTIONS
Une fraction est la notation d’un quotient de deux nombres entiers. Le trait de fraction représente une division. Un fraction est sous la forme
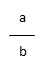
a => numérateur
b => dénominateur
Bases :

On appelle fraction inverse d’une fraction, la fraction dont le numérateur et le dénominateur sont inversés :

Exemple :
0/6 = 0
6/6 = 1
6/1 = 6
6/2 est l’inverse de 2/6
Règle 1
Pour multiplier deux fractions, je multiplie leurs numérateurs entre eux et leurs dénominateurs entre eux :

Exemple :
2/4 x 1/3 = (2x1)/(4x3) = 2/12 = 1/6
Règle 2
Pour diviser deux fractions, je multiplie par l’inverse de la deuxième fraction :

Exemple :
(8/3) / (2/4) = 8/3 x 4/2 = (8x4) / (3x2) = 32/6 = 16/3
Règle 3
Si on retrouve un même nombre eu numérateur et au dénominateur d’une fraction, on peut simplifier la fraction, c'est-à-dire « éliminer » ce nombre au numérateur et au dénominateur de la fraction :

Exemple :
2/3 x 3/6 = (2x3)/(3x6) = 2/6 = 1/3
Règle 4
Pour additionner ou soustraire deux fractions, elles doivent avoir le même dénominateur.
Si les deux fractions n’ont pas le même dénominateur, je trouve un dénominateur commun.
Pour obtenir le dénominateur commun, on peut soit multiplier les deux dénominateurs entre eux, soit trouver un multiple commun aux deux dénominateurs.
Exemple :
2/8 + 10/4
On peux tout mettre sur 8 en multipliant la deuxième fraction par 2
2/8 + 20/8
On peux tout mettre sur 4 en divisant la première fraction par 2
1/4 + 10/4
On peut tout mettre sur 32 en multipliant la première par 4 et la seconde par 8
8/32 + 80/32
Peu importe la méthode que vous choisirez, le résultat sera toujours le même ! Du coup, choisir 2 versions différentes permet de contrôler si notre calcul est juste.
Règle 5
Pour additionner ou soustraire deux fractions qui ont le même dénominateur, on additionne ou soustrait leurs numérateurs et on garde le dénominateur commun :

Exemple :
8/32 + 80/32 = (8+80)/32 = 88/32 = 11/4
10/4 - 1/4 = (10-1)/4 = 9/4
Une fraction est la notation d’un quotient de deux nombres entiers. Le trait de fraction représente une division. Un fraction est sous la forme
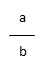
a => numérateur
b => dénominateur
Bases :

On appelle fraction inverse d’une fraction, la fraction dont le numérateur et le dénominateur sont inversés :

Exemple :
0/6 = 0
6/6 = 1
6/1 = 6
6/2 est l’inverse de 2/6
Règle 1
Pour multiplier deux fractions, je multiplie leurs numérateurs entre eux et leurs dénominateurs entre eux :

Exemple :
2/4 x 1/3 = (2x1)/(4x3) = 2/12 = 1/6
Règle 2
Pour diviser deux fractions, je multiplie par l’inverse de la deuxième fraction :

Exemple :
(8/3) / (2/4) = 8/3 x 4/2 = (8x4) / (3x2) = 32/6 = 16/3
Règle 3
Si on retrouve un même nombre eu numérateur et au dénominateur d’une fraction, on peut simplifier la fraction, c'est-à-dire « éliminer » ce nombre au numérateur et au dénominateur de la fraction :

Exemple :
2/3 x 3/6 = (2x3)/(3x6) = 2/6 = 1/3
Règle 4
Pour additionner ou soustraire deux fractions, elles doivent avoir le même dénominateur.
Si les deux fractions n’ont pas le même dénominateur, je trouve un dénominateur commun.
Pour obtenir le dénominateur commun, on peut soit multiplier les deux dénominateurs entre eux, soit trouver un multiple commun aux deux dénominateurs.
Exemple :
2/8 + 10/4
On peux tout mettre sur 8 en multipliant la deuxième fraction par 2
2/8 + 20/8
On peux tout mettre sur 4 en divisant la première fraction par 2
1/4 + 10/4
On peut tout mettre sur 32 en multipliant la première par 4 et la seconde par 8
8/32 + 80/32
Peu importe la méthode que vous choisirez, le résultat sera toujours le même ! Du coup, choisir 2 versions différentes permet de contrôler si notre calcul est juste.
Règle 5
Pour additionner ou soustraire deux fractions qui ont le même dénominateur, on additionne ou soustrait leurs numérateurs et on garde le dénominateur commun :

Exemple :
8/32 + 80/32 = (8+80)/32 = 88/32 = 11/4
10/4 - 1/4 = (10-1)/4 = 9/4
ESI 2013 / 2016 a Tours CHRU
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
- missdunord59
- Régulier

- Messages : 58
- Inscription : 22 févr. 2012 13:58
Re: Mathématiques concours 2013
Mon problème est les équations, je ne me pose pas les bonnes questions donc pas les bons calculs, je bûche depuis deux jours et je suis toujours incapable de faire un problème avec équation même simple aux dires de certains, exemple:
Lors des dernières élections municipales, 2518 habitants de village se sont exprimés.Le vainqueur est arrivé en tête avec 217 voix d'avance sur le second qui a obtenu lui même 150 voix d'avance sur le troisième.
Combien d'électeurs ont voté pour le vainqueur?
(source: tests d'aptitudes numériques, édition ellipses)
Si vous y arrivez toute explication et pour moi bonne à prendre.
Bon courage à tous et toutes
" Révisions quand tu nous tiens!!!!"
Lors des dernières élections municipales, 2518 habitants de village se sont exprimés.Le vainqueur est arrivé en tête avec 217 voix d'avance sur le second qui a obtenu lui même 150 voix d'avance sur le troisième.
Combien d'électeurs ont voté pour le vainqueur?
(source: tests d'aptitudes numériques, édition ellipses)
Si vous y arrivez toute explication et pour moi bonne à prendre.
Bon courage à tous et toutes
" Révisions quand tu nous tiens!!!!"
Concours 2018 me voici, cette fois sera la bonne, enfin j'espère ^^
être ESI => Mon objectif
être ESI => Mon objectif
- supercuisto
- Accro

- Messages : 1120
- Inscription : 05 mars 2012 20:37
Re: Mathématiques concours 2013
Ok c'est parti !missdunord59 a écrit :Mon problème est les équations, je ne me pose pas les bonnes questions donc pas les bons calculs, je bûche depuis deux jours et je suis toujours incapable de faire un problème avec équation même simple aux dires de certains, exemple:
Lors des dernières élections municipales, 2518 habitants de village se sont exprimés.Le vainqueur est arrivé en tête avec 217 voix d'avance sur le second qui a obtenu lui même 150 voix d'avance sur le troisième.
Combien d'électeurs ont voté pour le vainqueur?
(source: tests d'aptitudes numériques, édition ellipses)
Si vous y arrivez toute explication et pour moi bonne à prendre.
Bon courage à tous et toutes
" Révisions quand tu nous tiens!!!!"
Appelons chacun des candidats par une lettre A, B et C => A étant le vainqueur, et C celui qui a eu le moins de voie.
On nous dis que le candidat A a eu 217 voies de plus que B :
donc A = B +217
On nous dis que B a eu 150 voies de plus que C :
donc B = C +150
On sait aussi que A + B + C = 2518 voies (si on part du postula que tout le monde a voté, qu'il n'y a que 3 candidats et que personne ne vote blanc...)
Ensuite dans notre équation, on va remplacer A et B par nos formules du hat !
donc A + B + C = 2518
B+217 + C + 150 + C = 2518
ensuite on remplace le B restant par la formule du haut pour n'avoir que des C :
C +150 + 217 + C +150 + C = 2518
3 C + 517 = 2518
3 C = 2518 - 517
3 C = 2001
C = 200/3
C = 667
Donc on sait que B = C +150 = 667 + 150 = 817et on sait que A = B + 217 = 817 + 217 = 1034.
Les candidats ont donc récolté 1034 voies pour le premier, 817 pour le deuxième et 667 pour le dernier (ce qui fait bien un total de 2 518 voies)
Est ce que ça te convient ?
Dernière modification par supercuisto le 04 oct. 2012 14:24, modifié 1 fois.
ESI 2013 / 2016 a Tours CHRU
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
- missdunord59
- Régulier

- Messages : 58
- Inscription : 22 févr. 2012 13:58
Re: Mathématiques concours 2013
Alors là je dois te dire que je suis sur les fesses  , alors oui ça me convient merci pour ton explication c'est gentil de t'être penché sur mon cas... Il n'y a rien à faire, les maths même avec la meilleure des volontés s'est ma bête noire, merci encore
, alors oui ça me convient merci pour ton explication c'est gentil de t'être penché sur mon cas... Il n'y a rien à faire, les maths même avec la meilleure des volontés s'est ma bête noire, merci encore
Concours 2018 me voici, cette fois sera la bonne, enfin j'espère ^^
être ESI => Mon objectif
être ESI => Mon objectif









