Les maths pour le concours IFSI.

[ororr]

Oui c'est ça en fait c'est ça qui me manquait!! Le fait de soustraire les sommes.

En fait quand on fait 3 cercles qui se recoupent ça devient plus clair!!
Merci à vous en tout cas!!

[Leopold Anasthase]

Voici les résultats d'une enquète sur la lecture de 3 journaux A, B et C réalisée auprès de 100 personnes:
--> 6 personnes lisent A, B et C.
--> 35 lisent A, 50 lisent B, 39 lisent C.
--> 16 lisent A et B, 10 lisent B et C, 15 lisent A et C.

==> Combien ne lisent aucun journal?

==> Combien ne lisent que A?

==> Combien ne lisent que B?

C'est un problème d'ensembles et d'intersections. Le plus simple est de le résoudre de façon graphique.

Dessiner trois cercles entrelacés, par exemple comme ceci :



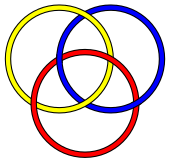
On conviendra que les lecteurs de A sont dans le cercle jaune, les lecteurs de B dans le cercle bleu, et les lecteurs de C dans le cercle rouge.

Il ne vous reste plus qu'à placer les nombres au bon endroit, en commençant par les intersections.

6 personnes lisent A, B et C

Commençons par placer les 6 qui lisent les trois journaux à l'intersection du centre (zone commune aux trois cercles. On écrit 6.

16 lisent A et B

Mais dans ces 16, on en a déjà placé 6 (qui lisent les trois journaux). Il faut donc en placer 10 qui lisent A et B, auxquels s'ajoutent 6 qui lisent A, B et C, ce qui fait bien 16 qui lisent A et B.

Refaire le même raisonnement pour les autres intersections.

Une fois les intersections placées, on place les lecteurs qui lisent A sans lire ni B ni C. On a "35 lisent A", mais également "16 lisent A et B", et "6 personnes lisent A, B et C". Il ne reste donc que 10 qui ne lisent que A.

Refaire le même raisonnement pour B et C. On obtient ainsi la réponse aux questions 2 et 3.

Ensuite, on fait le total de tous les lecteurs, on soustrait ce total de 100, et on obtient la réponse à la première question.

[ororr]

Voici les résultats d'une enquète sur la lecture de 3 journaux A, B et C réalisée auprès de 100 personnes:
--> 6 personnes lisent A, B et C.
--> 35 lisent A, 50 lisent B, 39 lisent C.
--> 16 lisent A et B, 10 lisent B et C, 15 lisent A et C.

==> Combien ne lisent aucun journal?

==> Combien ne lisent que A?

==> Combien ne lisent que B?

C'est un problème d'ensembles et d'intersections. Le plus simple est de le résoudre de façon graphique.

Dessiner trois cercles entrelacés, par exemple comme ceci :



On conviendra que les lecteurs de A sont dans le cercle jaune, les lecteurs de B dans le cercle bleu, et les lecteurs de C dans le cercle rouge.

Il ne vous reste plus qu'à placer les nombres au bon endroit, en commençant par les intersections.

6 personnes lisent A, B et C

Commençons par placer les 6 qui lisent les trois journaux à l'intersection du centre (zone commune aux trois cercles. On écrit 6.

16 lisent A et B

Mais dans ces 16, on en a déjà placé 6 (qui lisent les trois journaux). Il faut donc en placer 10 qui lisent A et B, auxquels s'ajoutent 6 qui lisent A, B et C, ce qui fait bien 16 qui lisent A et B.

Refaire le même raisonnement pour les autres intersections.

Une fois les intersections placées, on place les lecteurs qui lisent A sans lire ni B ni C. On a "35 lisent A", mais également "16 lisent A et B", et "6 personnes lisent A, B et C". Il ne reste donc que 10 qui ne lisent que A.

Refaire le même raisonnement pour B et C. On obtient ainsi la réponse aux questions 2 et 3.

Ensuite, on fait le total de tous les lecteurs, on soustrait ce total de 100, et on obtient la réponse à la première question.

Merci pour la réponse!! Avec les cercles c'est beaucoup plus simple...
En fait, 6 lisent A, B, C ; 10 lisent A et B (16-6) et 9 lisent A et C (15-6).
Donc pour trouver A:
35-6-10-9= 10...

Et puis pareil pour les autres...Merci beaucoup! et bonne soirée

[Marylène]

je ne trouve pas du tout comme vous , j'essaie juste de raisonner simplement , quand je vérifie mes calculs j'ai l'impression que c'est cohérent et finalement, j'ai tout faux.
Dites moi où mon raisonnement foire? Please

- combien ne lisent pas du tout : 22
je calcule d'abord ceux qui ne lisent que A B ou C :
A : 35 - (15-16) = 4
B : 50 - ( 16+10)= 24
C : 39 - ( 10+ 15) = 14

Dc 43 person qui ne lisent qu'un seul journal
s'il y a 100 personnes alors:

100 - ( 43 + 15 + 16 + 10 -6 ) = 100 - 78 = 22


en fait j'ai déjà répondu aux deux autres questions dans la première

- combien ne lisent que A : 4 ; que B : 24

[Leopold Anasthase]

je ne trouve pas du tout comme vous , j'essaie juste de raisonner simplement , quand je vérifie mes calculs j'ai l'impression que c'est cohérent et finalement, j'ai tout faux.
Dites moi où mon raisonnement foire?

Le problème est de compter les gens une fois et pas deux. Faites l'essai, faites un schéma avec des intersections, ça vous semblera limpide.

L'autre problème, c'est de bien comprendre l'énoncé. Si on vous dit "35 personnes lisent A", dans ces 35 personnes, il y a ceux qui ne lisent que A, ceux qui lisent A et B mais pas C, ceux qui lisent A et C mais pas B, et ceux qui lisent A, B et C.

[4611samsara]

c'est pas évident de poser des équations si vous n'avez pas l'habitude, et c'est même risqué car on peut se tromper.

moi j'ai bien réussi le concours et j'ai pu répondre à toutes les questions d'aptitude numérique simplement en partant des réponses proposées: tu vérifie et quand tu en une qui fonctionne, c'est la bonne.
mais il faut rester calme et concentrer, sinon rien ne vas plus!

[Dowbette]

Oui mais le hic, c'est que parfois il n'y a pas de propositions de réponses d'où l'importance de savoir déduire les équations en fonction de l'énoncé.

[fille]

voilà j'ai quelque soucis en math

Quatre ouvriers produisent 28 pièces en 5 jours. Combien d'ouvriers effectueraient le même travail en une demi-journée?

Une employée met 4 heures pour faire tous les lits d'un service. Sa collègue met la moitié de temps. En travaillant ensemble, à quelle heure finiront-elles en commençant à 8 h 52?

[Leopold Anasthase]

Avant propos : bonjour, je suis truc, je fais ça, j'ai tel soucis. C'est pas grand chose, ça prend deux lignes et ça met de l'huile dans les relations sociales.

Quatre ouvriers produisent 28 pièces en 5 jours. Combien d'ouvriers effectueraient le même travail en une demi-journée?

Encore un problème mal conçu. On ne peut pas établir de relation de proportionalité pour des variables non continue. Si on parle de temps, de masse, on peut le diviser autant de fois qu'on veut, ça garde un sens. Ça n'est pas le cas du travail en groupe. Je vais donc vous donner une réponse qui ne figure pas dans les cases à cocher.

Pour expliciter ma réponse, je l'illustre d'éléments concrets. Si le travail était une donnée continue, on se dirait que si 4 ouvriers produisent 28 pièces en 5 jours, et qu'on souhaite produire 28 pièces en une demi-journée, étant donné qu'une demi-journée c'est dix fois moins que 5 jours, il faudrait dix fois plus d'ouvriers. Mais...

Mais en fait on n'en sait rien. Par exemple, peut-être que chaque pièce nécessite cinq heures de travail et 3 heures de séchage. En une demi-journée, on produit zéro pièces, quel que soit le nombre d'ouvriers.

En résumé, ça n'est pas parce qu'on a deux fois plus d'ouvriers qu'on produit deux fois plus de travail, et ça n'est pas parce qu'on a deux fois moins d'ouvriers qu'on produit deux fois moins de travail.

[Leopold Anasthase]

Une employée met 4 heures pour faire tous les lits d'un service. Sa collègue met la moitié de temps. En travaillant ensemble, à quelle heure finiront-elles en commençant à 8 h 52?

Encore un problème sans intérêt, auquel on ne peut pas répondre.

Présenté comme ça, on peut penser que les employées vont faire les lits toutes seules.

Supposons qu'il n'y ait qu'un seul lit dans le service. Si c'est l'employée rapide qui le fait, elles auront finit en deux heures. Si c'est l'employée lente, ça prendra quatre heures.

S'il y a deux lits à faire, elles mettrons deux heures.

S'il y a trois lits à faire, la lente fait un lit en 80 minutes et la rapide en 40 minutes. Au bout de 80 minutes, la lente aura fait un lit et la rapide deux.

Et ainsi de suite.

[Ghyslaine]

bonjour ,je suis nouvelle sur le forum, je m'appelle ghyslaine, j'ai 29 ans et je prépare le concours depuis le mois de décembre, pour les maths je travaille avec le site de beltrame, une prépa du cned d'une copine, et des prépas livre.... il y a tellement de choses à voir...
vous vous préparez avec quoi?
à quel rythme?
vous avez des problèmes avec des convertions? c'est mon dernier gros soucis?
merci de me répondre

[Leopold Anasthase]

Allez, je vous propose deux problèmes de maths du niveau des concours d'entrée en ifsi.

Un tapis roulant permet de traverser un aérogare. Leopold l'emprunte souvent. Le problème, c'est qu'il ne fonctionne pas toujours.

Quand le tapis est en panne, Leopold met 4 minutes à le parcourir à pied en marchant.

Quand le tapis fonctionne et que Leopold n'a pas envie de marcher, Leopold met 5 minutes.

Quel temps mettra Leopold pour parcourir le tapis s'il fonctionne et s'il marche au même rythme que quand il ne fonctionne pas ?

Dans le même genre, un autre tapis, et toujours Leopold.

Si le tapis fonctionne et que Leopold marche, il met 2 minutes. Si le tapis fonctionne et que Leopold ne marche pas, il met 5 minutes.

Quel temps mettra Leopold à parcourir le tapis en marchant s'il marche et que le tapis ne fonctionne pas ?

[Ghyslaine]

dis donc, fainéant! franchement il ferait mieux de marcher au lieu d'attendre!

[Ghyslaine]

je rigole bien entendu, mais pour le problème je sèche, je réessaie aprés le repas des enfants

[fille]

moi jvois pas il fau utilisé T=d/v ????