Les maths pour le concours IFSI.
Modérateurs : Modérateurs, Concours IFSI
- supercuisto
- Accro

- Messages : 1120
- Inscription : 05 mars 2012 20:37
Re: Mathématiques concours 2013
LES PERIMETRES, AIRES ET VOLUMES.
FORMULES
Périmètres (circonférence) :
Le carré : 4 X c => (c = côté)
Le rectangle : 2 X (L+l) => (L = longueur ; l = largeur)
Le cercle : 2 X π X r ou π X D => (r = rayon ; D = diamètre ; π pi = 3.14 valeur approximative)
Aires (surfaces) :
Le carré : c²
Le rectangle : L X l
Le triangle : (b X h)/2 => (b = base ; h = hauteur)
Le cercle : π X r²
Volumes :
Les solides droits (cylindre, pavé, cube…) : A X h => (A = aire)
Les solides en pointes (pyramide, cône…) : (A X h)/3
Les sphères :
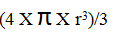
Exemples :
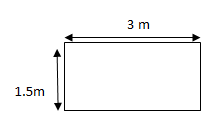
Le périmètre de ce rectangle :
2 x (L+l) = 2 x (3+1,5) = 2 x 4.5 = 9 m
Pensez toujours à bien indiquer l'unité de mesure dans votre réponse ! La bonne réponse n'est pas 9 mais 9 mètres.
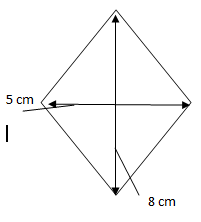
Aire de ce losange : (2 triangles superposés)
2 x [(bxh)/2] => le x2 et le /2 s'annulent, il reste donc 5x4 = 20 cm²
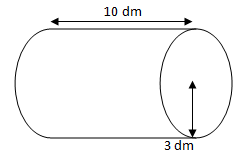
Aire de ce cylindre : A X h (NB : dans cet exo, Pi=3)
Aire du cercle de base : π X r²
A = 3 X 3² = 3 X 9 = 27 dm²
Volume = 27 X 10 = 270 dm3 (dm cube)
Dans le dernier exercice, il est écrit que π = 3. Cela arrive fréquemment dans les concours pour faciliter les calculs.
FORMULES
Périmètres (circonférence) :
Le carré : 4 X c => (c = côté)
Le rectangle : 2 X (L+l) => (L = longueur ; l = largeur)
Le cercle : 2 X π X r ou π X D => (r = rayon ; D = diamètre ; π pi = 3.14 valeur approximative)
Aires (surfaces) :
Le carré : c²
Le rectangle : L X l
Le triangle : (b X h)/2 => (b = base ; h = hauteur)
Le cercle : π X r²
Volumes :
Les solides droits (cylindre, pavé, cube…) : A X h => (A = aire)
Les solides en pointes (pyramide, cône…) : (A X h)/3
Les sphères :
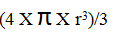
Exemples :

Le périmètre de ce rectangle :
2 x (L+l) = 2 x (3+1,5) = 2 x 4.5 = 9 m
Pensez toujours à bien indiquer l'unité de mesure dans votre réponse ! La bonne réponse n'est pas 9 mais 9 mètres.

Aire de ce losange : (2 triangles superposés)
2 x [(bxh)/2] => le x2 et le /2 s'annulent, il reste donc 5x4 = 20 cm²

Aire de ce cylindre : A X h (NB : dans cet exo, Pi=3)
Aire du cercle de base : π X r²
A = 3 X 3² = 3 X 9 = 27 dm²
Volume = 27 X 10 = 270 dm3 (dm cube)
Dans le dernier exercice, il est écrit que π = 3. Cela arrive fréquemment dans les concours pour faciliter les calculs.
ESI 2013 / 2016 a Tours CHRU
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
- supercuisto
- Accro

- Messages : 1120
- Inscription : 05 mars 2012 20:37
Re: Mathématiques concours 2013
Application aires, périmètres et volumes.
Exercices (corrigé dans prochain message)
On prend pour ces calculs pi=3
Périmètre d'un carré de 8m de côté
Périmètre d'un rectangle de Largeur = 8 cm et longueur = 3 cm
Périmètre d'un cercle de rayon = 6mm
Aire d'un carré de côté = 8m
Aire d'un rectangle de Largeur = 1m et largeur = 60 cm
Aire d'un triangle de base = 4 dam et hauteur = 2.5 dam
Aire d'un disque de diamètre = 6m
Volume d'un pavé de Longueur = 8cm, largeur = 4cm, hauteur = 2cm
Volume d'un cône de hauteur = 4dm, diamètre 10dm
Volume d'une sphère de 4cm de diamètre
Exercices (corrigé dans prochain message)
On prend pour ces calculs pi=3
Périmètre d'un carré de 8m de côté
Périmètre d'un rectangle de Largeur = 8 cm et longueur = 3 cm
Périmètre d'un cercle de rayon = 6mm
Aire d'un carré de côté = 8m
Aire d'un rectangle de Largeur = 1m et largeur = 60 cm
Aire d'un triangle de base = 4 dam et hauteur = 2.5 dam
Aire d'un disque de diamètre = 6m
Volume d'un pavé de Longueur = 8cm, largeur = 4cm, hauteur = 2cm
Volume d'un cône de hauteur = 4dm, diamètre 10dm
Volume d'une sphère de 4cm de diamètre
ESI 2013 / 2016 a Tours CHRU
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
- supercuisto
- Accro

- Messages : 1120
- Inscription : 05 mars 2012 20:37
Re: Mathématiques concours 2013
Corrigé des exercices sur périmètres, aires et volumes.
Périmètre d'un carré de 8m de côté
4 x c = 4 x 8 = 32 m
Périmètre d'un rectangle de Largeur = 8 cm et longueur = 3 cm
2 x (L+l) = 2 x (8+3) = 2 x 11 = 22 cm
Périmètre d'un cercle de rayon = 6mm
2 x Pi x r = 2 x 3 x 6 = 36 mm
Aire d'un carré de côté = 8m
c² = 8² = 64 m²
Aire d'un rectangle de Largeur = 1m et largeur = 60 cm
Petit piège dans cette question, il faut penser à mettre les données dans la même unité : soit en mètre soit en centimètre !
L x l = 1 x 0.6 = 0.6 m²
Aire d'un triangle de base = 4 dam et hauteur = 2.5 dam
(B x h) / 2 = (4 x 2.5) / 2 = 10/2 = 5 dam² (= 5 ares)
Aire d'un disque de diamètre = 6m
Petit piège aussi, on vous donne le diamètre alors que pour la formule il nous faut le rayon ; il faut donc penser à diviser par 2 le diamètre)
Pi x R² = 3 x 3² = 3 x 9 = 27 m²
Volume d'un pavé de Longueur = 8cm, largeur = 4cm, hauteur = 2cm
B x h La base ets un rectangle donc : B = L x l
(8 x 4) x 2 = 32 x 2 = 64 cm cube
Volume d'un cône de hauteur = 4dm, diamètre 10dm
Attention on vous donne le diamètre, penser à diviser par 2 pour obtenir le rayon pour les formules.
(Bx h)/3 La base est un disque donc : B = Pi x R²
[(3 x 5²) x 4]/3 = [(3 x 25)x4]/3 = (75 x4)/3 = 300/3 = 100 dm cube (=100 litres)
Volume d'une sphère de 4cm de diamètre
(4 x Pi x R au cube)/3 = (4 x 3 x 2 au cube)/3 = 96/3 = 32 cm cube
Périmètre d'un carré de 8m de côté
4 x c = 4 x 8 = 32 m
Périmètre d'un rectangle de Largeur = 8 cm et longueur = 3 cm
2 x (L+l) = 2 x (8+3) = 2 x 11 = 22 cm
Périmètre d'un cercle de rayon = 6mm
2 x Pi x r = 2 x 3 x 6 = 36 mm
Aire d'un carré de côté = 8m
c² = 8² = 64 m²
Aire d'un rectangle de Largeur = 1m et largeur = 60 cm
Petit piège dans cette question, il faut penser à mettre les données dans la même unité : soit en mètre soit en centimètre !
L x l = 1 x 0.6 = 0.6 m²
Aire d'un triangle de base = 4 dam et hauteur = 2.5 dam
(B x h) / 2 = (4 x 2.5) / 2 = 10/2 = 5 dam² (= 5 ares)
Aire d'un disque de diamètre = 6m
Petit piège aussi, on vous donne le diamètre alors que pour la formule il nous faut le rayon ; il faut donc penser à diviser par 2 le diamètre)
Pi x R² = 3 x 3² = 3 x 9 = 27 m²
Volume d'un pavé de Longueur = 8cm, largeur = 4cm, hauteur = 2cm
B x h La base ets un rectangle donc : B = L x l
(8 x 4) x 2 = 32 x 2 = 64 cm cube
Volume d'un cône de hauteur = 4dm, diamètre 10dm
Attention on vous donne le diamètre, penser à diviser par 2 pour obtenir le rayon pour les formules.
(Bx h)/3 La base est un disque donc : B = Pi x R²
[(3 x 5²) x 4]/3 = [(3 x 25)x4]/3 = (75 x4)/3 = 300/3 = 100 dm cube (=100 litres)
Volume d'une sphère de 4cm de diamètre
(4 x Pi x R au cube)/3 = (4 x 3 x 2 au cube)/3 = 96/3 = 32 cm cube
ESI 2013 / 2016 a Tours CHRU
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
- supercuisto
- Accro

- Messages : 1120
- Inscription : 05 mars 2012 20:37
Re: Mathématiques concours 2013
DECOMPOSITION EN FACTEURS PREMIERS, LE PGCD ET LE PPCM.
Tout d’abord, on dit d’un nombre qu’il est premier s’il ne peut être divisé que par 1 et par lui même. (par exemple 3 est un nombre premier)
La décomposition en facteurs premiers d’un nombre est le fait d’écrire ce nombre sous la forme d’ un produit de nombres, les plus petits possibles. (en clair, c’est écrire ce nombre sous la forme d’une multiplication de nombres les plus petits possibles)
Exemple :
La décomposition en facteurs premiers de 12 est 2 x 2 x 3.
Cela peut vous servir aussi bien dans des calculs de fractions et de racines carrées que dans la résolution de certains problèmes mathématiques. On se sert également de cette décomposition pour le calcul des PGCD et PPCM.
Que signifient ces initiales ?
Le PGCD de plusieurs nombres est le Plus Grand Commun Diviseur de ces nombres ; c’est le plus grand nombre possible qui peut diviser tous ces nombres à la fois.
Le PPCM de plusieurs nombres est le Plus Petit Commun Multiple de ces nombres ; c’est le plus petit nombre possible qui est un multiple de tous ces nombres.
Ces deux grandeurs sont très utiles pour les calculs sur les fractions (le PPCM permet de calculer le dénominateur commun à plusieurs fractions), mais également pour résoudre certains problèmes mathématiques.
D’abord, les astuces :
Un premier conseil pour réussir à effectuer de tels calculs est de connaître parfaitement ses tables de multiplication (cf. la leçon sur le calcul de base).
Un second conseil est de connaître les critères de divisibilité des nombres : ce sont des astuces qui vous permettent de savoir rapidement par quel(s) chiffre(s) on peut diviser un nombre !
Astuce 1 :
Un nombre est divisible par 2 s’il se termine par un chiffre pair.
Exemple :
1236 => finit par un chiffre pair (6) il est donc divisible par 2. => 1236/2 = 618
Astuce 2 :
Un nombre est divisible par 3 si la somme des chiffres qui le composent est un multiple de 3.
Exemple :
369 => 3+6+9=18 => 1+8=9 => 9 est multiple de 3 (3x3) donc 369 est divisible par 3 =>369/3=123
Astuce 3 :
Un nombre est divisible par 9 si la somme des chiffres qui le composent est un multiple de 9.
Exemple :
369 => 3+6+9=18 => 18 est multiple de 9 (9x2) => donc 369 est divisible par 9 => 369/9=41
Ces astuces sont très utiles pour trouver la décomposition en nombres premiers d’un nombre donné. Cette décomposition nous servira au calcul du PGCD et du PPCM de plusieurs nombres.
Les calculs de PGCD et PPCM permettent de répondre à 2 sortes de problèmes courants :
1. Je veux compter le nombre maximum de « paquets » identiques que je peux faire avec différents objets disponibles dans des quantités différentes. Dans ce cas, je calcule le PGCD des différentes quantités.
Règle 1 : S’il s’agit de 2 quantités différentes, je procède par division successives. Je divise la plus grande par la plus petite, puis je divise le diviseur (la plus petite quantité) par le reste de la division précédente etc. jusqu’à un reste nul. Le PGCD est alors le dernier diviseur.
Exemple :
Je dispose de 36 bonbons rouges et de 27 bonbons verts, et je veux faire un maximum de paquets, tous identiques, contenant des bonbons des 2 couleurs.
Je dois calculer le PGCD de 36 et 27.

Je divise le plus grand chiffre (36) par le plus petit (27).
Ensuite, je divise le plus petit (27) par le reste de la division précédente (9).
Si le reste de cette opération est égal à 0, alors ce dernier diviseur (9) est le PGCD.
Le PGCD de 36 et 27 est 9. On pourra faire 9 paquets ; ils contiendront 4 bonbons rouges (36/9 = 4) et 3 bonbons verts (27/9 = 3).
Règle 2 : S’il s’agit de plus de deux quantités différentes, je trouve la décomposition en facteurs premiers des différentes quantités. Le PGCD est alors le produit des facteurs communs aux différentes quantités.
Exemple :
Je veux calculer le PGCD de 45,30 et 165.
On va décomposer ces trois nombres en facteurs premiers. On les divise pour cela successivement par des nombres premiers.
45/3 = 15 => 15/3= 5 => 5/5=1 => donc 45 = 3 x 3 x 5
30/2 = 15 => 15/3 = 5 => 5/5 = 1 => donc 30 = 2 x 3 x 5
165/3 = 55 => 55/5 = 11 => 11/11 = 1 =>donc 165 = 3 x 5 x 11
On cherche alors les facteurs communs que l’on retrouve dans toutes les opérations (ici 3 et 5).
Le PGCD de 45,30 et 165 est donc 3 x 5 = 15
2. Je veux compter le temps minimum au bout duquel des évènements se produisant à différents intervalles se produiront au même moment. Je calcul le PPCM des différents temps.
Règle 3 : Je trouve la décomposition en facteurs premiers des différents temps. Le PPCM est alors le produit des facteurs qui composent ces nombres, en n’utilisant qu’une seule fois les facteurs se répétant dans les différents nombres.
Exemple :
Deux cloches commencent à sonner au même moment. La première sonne toutes les 14 secondes et la deuxième toutes les 4 secondes. Quand sonneront-elles à nouveau ensemble ?
On doit calculer le PPCM de 4 et 14 ; pour cela, on décompose 4 et 14 en facteurs premiers.
4 / 2 = 2 => 2 / 2 = 1 donc 4 décomposé en facteurs premiers = 2 x 2
14 / 2 = 7 => 7/7 = 1 donc 14 décomposé en facteurs premiers = 2 x 7
Il suffit alors de multiplier les chiffres obtenus entre eux (en ne prenant qu’une fois les chiffres communs, donc le 2 qui se trouve dans les deux formules ne se contera qu’une fois)
Donc , le PPCM de 14 et 4 est 2 x 2 x 7 = 28
Les cloches sonneront de nouveau ensemble au bout de 28 secondes.
Tout d’abord, on dit d’un nombre qu’il est premier s’il ne peut être divisé que par 1 et par lui même. (par exemple 3 est un nombre premier)
La décomposition en facteurs premiers d’un nombre est le fait d’écrire ce nombre sous la forme d’ un produit de nombres, les plus petits possibles. (en clair, c’est écrire ce nombre sous la forme d’une multiplication de nombres les plus petits possibles)
Exemple :
La décomposition en facteurs premiers de 12 est 2 x 2 x 3.
Cela peut vous servir aussi bien dans des calculs de fractions et de racines carrées que dans la résolution de certains problèmes mathématiques. On se sert également de cette décomposition pour le calcul des PGCD et PPCM.
Que signifient ces initiales ?
Le PGCD de plusieurs nombres est le Plus Grand Commun Diviseur de ces nombres ; c’est le plus grand nombre possible qui peut diviser tous ces nombres à la fois.
Le PPCM de plusieurs nombres est le Plus Petit Commun Multiple de ces nombres ; c’est le plus petit nombre possible qui est un multiple de tous ces nombres.
Ces deux grandeurs sont très utiles pour les calculs sur les fractions (le PPCM permet de calculer le dénominateur commun à plusieurs fractions), mais également pour résoudre certains problèmes mathématiques.
D’abord, les astuces :
Un premier conseil pour réussir à effectuer de tels calculs est de connaître parfaitement ses tables de multiplication (cf. la leçon sur le calcul de base).
Un second conseil est de connaître les critères de divisibilité des nombres : ce sont des astuces qui vous permettent de savoir rapidement par quel(s) chiffre(s) on peut diviser un nombre !
Astuce 1 :
Un nombre est divisible par 2 s’il se termine par un chiffre pair.
Exemple :
1236 => finit par un chiffre pair (6) il est donc divisible par 2. => 1236/2 = 618
Astuce 2 :
Un nombre est divisible par 3 si la somme des chiffres qui le composent est un multiple de 3.
Exemple :
369 => 3+6+9=18 => 1+8=9 => 9 est multiple de 3 (3x3) donc 369 est divisible par 3 =>369/3=123
Astuce 3 :
Un nombre est divisible par 9 si la somme des chiffres qui le composent est un multiple de 9.
Exemple :
369 => 3+6+9=18 => 18 est multiple de 9 (9x2) => donc 369 est divisible par 9 => 369/9=41
Ces astuces sont très utiles pour trouver la décomposition en nombres premiers d’un nombre donné. Cette décomposition nous servira au calcul du PGCD et du PPCM de plusieurs nombres.
Les calculs de PGCD et PPCM permettent de répondre à 2 sortes de problèmes courants :
1. Je veux compter le nombre maximum de « paquets » identiques que je peux faire avec différents objets disponibles dans des quantités différentes. Dans ce cas, je calcule le PGCD des différentes quantités.
Règle 1 : S’il s’agit de 2 quantités différentes, je procède par division successives. Je divise la plus grande par la plus petite, puis je divise le diviseur (la plus petite quantité) par le reste de la division précédente etc. jusqu’à un reste nul. Le PGCD est alors le dernier diviseur.
Exemple :
Je dispose de 36 bonbons rouges et de 27 bonbons verts, et je veux faire un maximum de paquets, tous identiques, contenant des bonbons des 2 couleurs.
Je dois calculer le PGCD de 36 et 27.

Je divise le plus grand chiffre (36) par le plus petit (27).
Ensuite, je divise le plus petit (27) par le reste de la division précédente (9).
Si le reste de cette opération est égal à 0, alors ce dernier diviseur (9) est le PGCD.
Le PGCD de 36 et 27 est 9. On pourra faire 9 paquets ; ils contiendront 4 bonbons rouges (36/9 = 4) et 3 bonbons verts (27/9 = 3).
Règle 2 : S’il s’agit de plus de deux quantités différentes, je trouve la décomposition en facteurs premiers des différentes quantités. Le PGCD est alors le produit des facteurs communs aux différentes quantités.
Exemple :
Je veux calculer le PGCD de 45,30 et 165.
On va décomposer ces trois nombres en facteurs premiers. On les divise pour cela successivement par des nombres premiers.
45/3 = 15 => 15/3= 5 => 5/5=1 => donc 45 = 3 x 3 x 5
30/2 = 15 => 15/3 = 5 => 5/5 = 1 => donc 30 = 2 x 3 x 5
165/3 = 55 => 55/5 = 11 => 11/11 = 1 =>donc 165 = 3 x 5 x 11
On cherche alors les facteurs communs que l’on retrouve dans toutes les opérations (ici 3 et 5).
Le PGCD de 45,30 et 165 est donc 3 x 5 = 15
2. Je veux compter le temps minimum au bout duquel des évènements se produisant à différents intervalles se produiront au même moment. Je calcul le PPCM des différents temps.
Règle 3 : Je trouve la décomposition en facteurs premiers des différents temps. Le PPCM est alors le produit des facteurs qui composent ces nombres, en n’utilisant qu’une seule fois les facteurs se répétant dans les différents nombres.
Exemple :
Deux cloches commencent à sonner au même moment. La première sonne toutes les 14 secondes et la deuxième toutes les 4 secondes. Quand sonneront-elles à nouveau ensemble ?
On doit calculer le PPCM de 4 et 14 ; pour cela, on décompose 4 et 14 en facteurs premiers.
4 / 2 = 2 => 2 / 2 = 1 donc 4 décomposé en facteurs premiers = 2 x 2
14 / 2 = 7 => 7/7 = 1 donc 14 décomposé en facteurs premiers = 2 x 7
Il suffit alors de multiplier les chiffres obtenus entre eux (en ne prenant qu’une fois les chiffres communs, donc le 2 qui se trouve dans les deux formules ne se contera qu’une fois)
Donc , le PPCM de 14 et 4 est 2 x 2 x 7 = 28
Les cloches sonneront de nouveau ensemble au bout de 28 secondes.
ESI 2013 / 2016 a Tours CHRU
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
Re: Mathématiques concours 2013
Salut,
je souhaiterai savoir s'il y a aussi de la géométrie dans le concours.
Je suis en terminal littéraire et je pense avoir beaucoup de chose à rattraper!
je souhaiterai savoir s'il y a aussi de la géométrie dans le concours.
Je suis en terminal littéraire et je pense avoir beaucoup de chose à rattraper!
Concours infirmier 2014 !
- supercuisto
- Accro

- Messages : 1120
- Inscription : 05 mars 2012 20:37
Re: Mathématiques concours 2013
a priori il y a parfois les calculs d'aires ou de volume dans des problèmes (comme j'ai deja mis la leçon).Shrayna a écrit :Salut,
je souhaiterai savoir s'il y a aussi de la géométrie dans le concours.
Je suis en terminal littéraire et je pense avoir beaucoup de chose à rattraper!
Mais après si c'est un aspect que tu ne maitrise pas je pense que c'est pas un drame car y'a tellement de questions que tu peux te rattraper ailleurs !
ESI 2013 / 2016 a Tours CHRU
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
Re: Mathématiques concours 2013
bonjour tout le monde
je vous suis depuis un moment sur "maman 2013, cultureG et donc math
ma question va droit à Supercuisto, tu as l'air de bien gérer tout ça
je suis en train de faire la prépa par le cned, et pas facile. je me suis établie un planning jusqu'à décembre mais maintenant je doute.
j'ai le lundi, mercredi et jeudi pour bucher, donc j'ai mis le lundi culture G, le mercredi test psy et jeudi maths
maintenant je commence à douter, dois je faire tous mes test d'abord, et après culture G ou inversement. ou est ce bien de faire un jour une matière?
sérieusement, je me fais peur, je sais plus
est ce que tu peux me conseiller? ou si quelqu'un a une méthode svp?
merci d'avance pour vos réponses
je vous suis depuis un moment sur "maman 2013, cultureG et donc math
ma question va droit à Supercuisto, tu as l'air de bien gérer tout ça
je suis en train de faire la prépa par le cned, et pas facile. je me suis établie un planning jusqu'à décembre mais maintenant je doute.
j'ai le lundi, mercredi et jeudi pour bucher, donc j'ai mis le lundi culture G, le mercredi test psy et jeudi maths
maintenant je commence à douter, dois je faire tous mes test d'abord, et après culture G ou inversement. ou est ce bien de faire un jour une matière?
sérieusement, je me fais peur, je sais plus
est ce que tu peux me conseiller? ou si quelqu'un a une méthode svp?
merci d'avance pour vos réponses
- supercuisto
- Accro

- Messages : 1120
- Inscription : 05 mars 2012 20:37
Re: Mathématiques concours 2013
oh tu sais je ne prétends pas avoir la bonne méthode ! en plus je n'ai pas encore passer le concours et mes études sont loin... (en plus j'ai fais mes études en cuisine !) mais les maths n'ont jamais été un probleme pour moi !
en tout cas je pense que c'est bon de varier les thèmes car si tu bosse que sur la CG pendant plusieurs jours ca va vite te gaver et te décourager ! je pense que c'est mieux d'alterner !
en meme temps je n'ai pas encore fait mon planning ! va falloir que j'y pense sérieusement !
en tout cas je pense que c'est bon de varier les thèmes car si tu bosse que sur la CG pendant plusieurs jours ca va vite te gaver et te décourager ! je pense que c'est mieux d'alterner !
en meme temps je n'ai pas encore fait mon planning ! va falloir que j'y pense sérieusement !
ESI 2013 / 2016 a Tours CHRU
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
-
Maëlle70400
- Messages : 1
- Inscription : 12 sept. 2012 11:10
Re: Mathématiques concours 2013
Bonjour Lala43140, je suis intéressée par un de vos livre : Les maths du concours infirmier édition Lamarre 2012.
Je suis nouvelle sur Infirmiers.com est j'avoue que je ne sais pas trop comment sa fonctionne. Est ce possible d'envoyer des messages privés ?
Merci, ce forum est très intéressant !!
Je suis nouvelle sur Infirmiers.com est j'avoue que je ne sais pas trop comment sa fonctionne. Est ce possible d'envoyer des messages privés ?
Merci, ce forum est très intéressant !!
Re: Mathématiques concours 2013
bonjour
merci supercuisto pour ta réponse
jen reviens pas comme on oublie vite tout ce que l'on a appris étant petit!
me remettre dans les nombres fractionnaires et cie c'est dépitant!
les maths c'est pas pour moi!j'ai du mal! et pourtant il faut!
les cours que vous postez sont vraiment bien fait merci
merci supercuisto pour ta réponse
jen reviens pas comme on oublie vite tout ce que l'on a appris étant petit!
me remettre dans les nombres fractionnaires et cie c'est dépitant!
les maths c'est pas pour moi!j'ai du mal! et pourtant il faut!
les cours que vous postez sont vraiment bien fait merci
-
noemie.lenglet
- Messages : 7
- Inscription : 30 août 2012 19:13
Mathématiques
Bonjour ,
Malgrés les livres , les exos j'ai toujours autant de mal avec les maths et sincérement sa me décourage énormément...
J'ai été sur pleins de site et toujours aussi difficile de comprendre , auriez vous des sites , des exos , des livres à me conseiller?
Je ne comprends rien au polynome, les équations du second degré etc... aidez moi svp
Merci d'avance.
Malgrés les livres , les exos j'ai toujours autant de mal avec les maths et sincérement sa me décourage énormément...
J'ai été sur pleins de site et toujours aussi difficile de comprendre , auriez vous des sites , des exos , des livres à me conseiller?
Je ne comprends rien au polynome, les équations du second degré etc... aidez moi svp
Merci d'avance.
- Miiniiimoy's
- Messages : 4
- Inscription : 15 août 2012 13:28
Re: Mathématiques concours 2013
Merci beaucoup pour ce topic ! A hâte de voir la suite du programme...
Prépare le concours IDE pour 2013...
Re: Mathématiques
Courage Noémie, moi aussi c'est ma bête noire, mais nous ne sommes pas plus bête que la moyenne alors on va y arriver.
Regarde, dans le forum, Supercuisto à ouvert un topic sur les maths qui est super
Sinon tu as
http://www.gomath.ch/
Et
http://www.mathematiquesfaciles.com/
Deux sites que je trouve très sympathique, le premier tu peux t'y exercer et le deuxième tu as également de la théorie.
Tu me diras ce que tu en penses

Regarde, dans le forum, Supercuisto à ouvert un topic sur les maths qui est super
Sinon tu as
http://www.gomath.ch/
Et
http://www.mathematiquesfaciles.com/
Deux sites que je trouve très sympathique, le premier tu peux t'y exercer et le deuxième tu as également de la théorie.
Tu me diras ce que tu en penses
Il est temps que je vive la vie que je m'étais imaginée
ESI 2013-2016 Antoine Béclere 2è année
S1 - psychiatrie
S2 - gériatrie chirurgie gynéco
S3 - hôpital pénitencier gériatrie
S4 - Pool
ESI 2013-2016 Antoine Béclere 2è année
S1 - psychiatrie
S2 - gériatrie chirurgie gynéco
S3 - hôpital pénitencier gériatrie
S4 - Pool
- supercuisto
- Accro

- Messages : 1120
- Inscription : 05 mars 2012 20:37
Re: Mathématiques concours 2013
Merci !
je vais essayer de remettre un cours ce soir mais je ne promets rien car ça prend beaucoup de temps !
je vais essayer de remettre un cours ce soir mais je ne promets rien car ça prend beaucoup de temps !
ESI 2013 / 2016 a Tours CHRU
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
En reconversion professionnelle... j'y crois !!!
S1 : EHPAD - 30 ECTS/30
S2 : DERMATOLOGIE
-
noemie.lenglet
- Messages : 7
- Inscription : 30 août 2012 19:13
Re: Mathématiques
Ha je me sent moins seule alors:)
je n'avais pas été sur go maths c'est vraiment pas mal merci beaucoup:)
tu le passe ou le concours en 2013?
je n'avais pas été sur go maths c'est vraiment pas mal merci beaucoup:)
tu le passe ou le concours en 2013?







