Question de maths à destination des "têtes"....

[Dowbette]

voici un autre: un wagon rempli de marchandises pèse 38 tonnes. Il ne pèse plus que 17 tonnes lorsqu'on a visé les 3/4 de son chargement. Combien pèse le wagon vide?

x = chargement

21 = 3/4 x
21/3 = 7
7 * 4 = 28
38 - 28 = 10 tonnesÉquipe de modération : Ce topic a été verrouillé et déplacé car il a déjà été traité et/ou ne figure pas dans le bon forum. Merci de consulter ce lien pour lire la suite.

[Leopold Anasthase]

un wagon rempli de marchandises pèse 38 tonnes. Il ne pèse plus que 17 tonnes lorsqu'on a visé les 3/4 de son chargement. Combien pèse le wagon vide?

x = chargement

21 = 3/4 x
21/3 = 7
7 * 4 = 28
38 - 28 = 10 tonnes

Bien joué. Le piège était de ne pas s'embrouiller entre chargement et wagon vide.Équipe de modération : Ce topic a été verrouillé et déplacé car il a déjà été traité et/ou ne figure pas dans le bon forum. Merci de consulter ce lien pour lire la suite.

[Dowbette]

exo guide masson 2e edition tests psycho
un immeuble comprend x appartements se repartissant en appartements de 2,3,4 et 5 pieces .il y a 5 fois moins d appart de 5 pieces que de 2 pieces.et 3 fois plus d appart de 4 pieces que de 5 pieces.sachant qu il y a moitie moins d appart de 3 pieces que de 2 pieces ,calculer le nombre d appart de 2 pieces.
la reponse est 10x/23
qui veut bien eclairer ma lanterne car je ne comprend pas le cheminement pour arriver a ce resultat.(ds le livre il n y a pas d explication)
merci aux matheux qui pourront repondre.

Équipe de modération : Ce topic a été verrouillé et déplacé car il a déjà été traité et/ou ne figure pas dans le bon forum. Merci de consulter ce lien pour lire la suite.

[Leopold Anasthase]

un immeuble comprend x appartements se repartissant en appartements de 2,3,4 et 5 pieces .il y a 5 fois moins d appart de 5 pieces que de 2 pieces.et 3 fois plus d appart de 4 pieces que de 5 pieces.sachant qu il y a moitie moins d appart de 3 pieces que de 2 pieces ,calculer le nombre d appart de 2 pieces.

Il faut définir les variables et traduire l'énoncé en équations.

Soit D le nombre d'appartements de deux pièces,
soit T le nombre d'appartements de trois pièces,
soit Q le nombre d'appartements de quatre pièces,
soit C le nombre d'appartements de cinq pièces.

On a :
1) Le nombre total d'appartements est égal à X

X = D + T + Q + C

2) Il y a cinq fois moins d'appartements de 5 pièces que de 2 pièces. Donc il y a cinq fois plus de deux pièces que de 5 pièces. On a :

D = 5 x C

Continuer ainsi avec les autres données. Au total, on obtient quatre équations pour cinq inconnues. Il est donc impossible de donner une réponse, mais on peut établir un rapport de proportionnalité entre les inconnues. On peut compléter la réponse en donnant la première réponse possible. En effet, il y a un élément supplémentaire : toutes les inconnues sont des entiers positifs.Équipe de modération : Ce topic a été verrouillé et déplacé car il a déjà été traité et/ou ne figure pas dans le bon forum. Merci de consulter ce lien pour lire la suite.

[foulcroule]

merci leo je m etais embrouiller pour nommer x(je nommais x nbre de 2 pieces)
avec ton explication j ai reussi.je revise beaucoup mais parfois j ai l impression de ne pas avancer comme ds ces cas la ou je me sens coince.ca fait 11 ans que j ai arrete les cours et en plus c etait un bac pro ou le niveau des maths est moyen.
vive les forums
ciaoÉquipe de modération : Ce topic a été verrouillé et déplacé car il a déjà été traité et/ou ne figure pas dans le bon forum. Merci de consulter ce lien pour lire la suite.

[cedr1c]

Cela reste un niveau fin de collège/ secondeÉquipe de modération : Ce topic a été verrouillé et déplacé car il a déjà été traité et/ou ne figure pas dans le bon forum. Merci de consulter ce lien pour lire la suite.

[Leopold Anasthase]

avec ton explication j ai reussi.

Ce qui serait bien, c'est que vous écriviez ici la fin de la démarche. Vous pouvez l'écrire en clair, mais vous pouvez aussi l'écrire en blanc ou en très petit, ceci afin de laisser ceux que le problème intéresserait chercher la solution avant de regarder la réponse. En plus, ça permet que d'autres s'inspirent de votre méthode, ou vous proposent une autre façon de faire.Équipe de modération : Ce topic a été verrouillé et déplacé car il a déjà été traité et/ou ne figure pas dans le bon forum. Merci de consulter ce lien pour lire la suite.

[ororr]

Bonjour tout le monde!!

Alors voilà je sèche sur une question de logique que j'ai dans mon bouquin. J'ai la réponse mais j'ai du mal à avoir le raisonnement. Voici le problème:

"Voici les résultats d'une enquète sur la lecture de 3 journaux A, B et C réalisée auprès de 100 personnes:
--> 6 personnes lisent A, B et C.
--> 35 lisent A, 50 lisent B, 39 lisent C.
--> 16 lisent A et B, 10 lisent B et C, 15 lisent A et C.

Combien ne lisent aucun journal?
Combien ne lisent que A?
Combien ne lisent que B?"

Voilou j'attends votre aide avec impatience!!! Équipe de modération : Ce topic a été verrouillé et déplacé car il a déjà été traité et/ou ne figure pas dans le bon forum. Merci de consulter ce lien pour lire la suite.

[Dolliprane]

Bonjour tout le monde!!

Alors voilà je sèche sur une question de logique que j'ai dans mon bouquin. J'ai la réponse mais j'ai du mal à avoir le raisonnement. Voici le problème:

"Voici les résultats d'une enquète sur la lecture de 3 journaux A, B et C réalisée auprès de 100 personnes:
--> 6 personnes lisent A, B et C.
--> 35 lisent A, 50 lisent B, 39 lisent C.
--> 16 lisent A et B, 10 lisent B et C, 15 lisent A et C.

Combien ne lisent aucun journal?
Combien ne lisent que A?
Combien ne lisent que B?"

Voilou j'attends votre aide avec impatience!!!

Combien ne lisent aucun journal: 35
Combien ne lisent que A : 13
Combien ne lisent que B: 34

C'est ça ?Équipe de modération : Ce topic a été verrouillé et déplacé car il a déjà été traité et/ou ne figure pas dans le bon forum. Merci de consulter ce lien pour lire la suite.

[ororr]

Non désolée!!

Les réponses sont respectivement 11, 10 et 30. Équipe de modération : Ce topic a été verrouillé et déplacé car il a déjà été traité et/ou ne figure pas dans le bon forum. Merci de consulter ce lien pour lire la suite.

[nygel]

je suis daccord avec ororr
jai trouvé 10 et 30 pour les questions 2 et 3, mais la 1 pas réussi, je cherche Équipe de modération : Ce topic a été verrouillé et déplacé car il a déjà été traité et/ou ne figure pas dans le bon forum. Merci de consulter ce lien pour lire la suite.

[Dolliprane]

Non désolée!!

Les réponses sont respectivement 11, 10 et 30.

Alors pour A

35-16-15+6=10

Alors pour B

50-16-10+6=30

Alors pour C

39-10-15+6=20Équipe de modération : Ce topic a été verrouillé et déplacé car il a déjà été traité et/ou ne figure pas dans le bon forum. Merci de consulter ce lien pour lire la suite.

[ororr]

Oui c'est ça en fait c'est ça qui me manquait!! Le fait de soustraire les sommes.

En fait quand on fait 3 cercles qui se recoupent ça devient plus clair!!
Merci à vous en tout cas!! Équipe de modération : Ce topic a été verrouillé et déplacé car il a déjà été traité et/ou ne figure pas dans le bon forum. Merci de consulter ce lien pour lire la suite.

[Leopold Anasthase]

Voici les résultats d'une enquète sur la lecture de 3 journaux A, B et C réalisée auprès de 100 personnes:
--> 6 personnes lisent A, B et C.
--> 35 lisent A, 50 lisent B, 39 lisent C.
--> 16 lisent A et B, 10 lisent B et C, 15 lisent A et C.

==> Combien ne lisent aucun journal?

==> Combien ne lisent que A?

==> Combien ne lisent que B?

C'est un problème d'ensembles et d'intersections. Le plus simple est de le résoudre de façon graphique.

Dessiner trois cercles entrelacés, par exemple comme ceci :



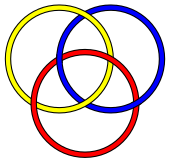
On conviendra que les lecteurs de A sont dans le cercle jaune, les lecteurs de B dans le cercle bleu, et les lecteurs de C dans le cercle rouge.

Il ne vous reste plus qu'à placer les nombres au bon endroit, en commençant par les intersections.

6 personnes lisent A, B et C

Commençons par placer les 6 qui lisent les trois journaux à l'intersection du centre (zone commune aux trois cercles. On écrit 6.

16 lisent A et B

Mais dans ces 16, on en a déjà placé 6 (qui lisent les trois journaux). Il faut donc en placer 10 qui lisent A et B, auxquels s'ajoutent 6 qui lisent A, B et C, ce qui fait bien 16 qui lisent A et B.

Refaire le même raisonnement pour les autres intersections.

Une fois les intersections placées, on place les lecteurs qui lisent A sans lire ni B ni C. On a "35 lisent A", mais également "16 lisent A et B", et "6 personnes lisent A, B et C". Il ne reste donc que 10 qui ne lisent que A.

Refaire le même raisonnement pour B et C. On obtient ainsi la réponse aux questions 2 et 3.

Ensuite, on fait le total de tous les lecteurs, on soustrait ce total de 100, et on obtient la réponse à la première question.Équipe de modération : Ce topic a été verrouillé et déplacé car il a déjà été traité et/ou ne figure pas dans le bon forum. Merci de consulter ce lien pour lire la suite.

[ororr]

Voici les résultats d'une enquète sur la lecture de 3 journaux A, B et C réalisée auprès de 100 personnes:
--> 6 personnes lisent A, B et C.
--> 35 lisent A, 50 lisent B, 39 lisent C.
--> 16 lisent A et B, 10 lisent B et C, 15 lisent A et C.

==> Combien ne lisent aucun journal?

==> Combien ne lisent que A?

==> Combien ne lisent que B?

C'est un problème d'ensembles et d'intersections. Le plus simple est de le résoudre de façon graphique.

Dessiner trois cercles entrelacés, par exemple comme ceci :



On conviendra que les lecteurs de A sont dans le cercle jaune, les lecteurs de B dans le cercle bleu, et les lecteurs de C dans le cercle rouge.

Il ne vous reste plus qu'à placer les nombres au bon endroit, en commençant par les intersections.

6 personnes lisent A, B et C

Commençons par placer les 6 qui lisent les trois journaux à l'intersection du centre (zone commune aux trois cercles. On écrit 6.

16 lisent A et B

Mais dans ces 16, on en a déjà placé 6 (qui lisent les trois journaux). Il faut donc en placer 10 qui lisent A et B, auxquels s'ajoutent 6 qui lisent A, B et C, ce qui fait bien 16 qui lisent A et B.

Refaire le même raisonnement pour les autres intersections.

Une fois les intersections placées, on place les lecteurs qui lisent A sans lire ni B ni C. On a "35 lisent A", mais également "16 lisent A et B", et "6 personnes lisent A, B et C". Il ne reste donc que 10 qui ne lisent que A.

Refaire le même raisonnement pour B et C. On obtient ainsi la réponse aux questions 2 et 3.

Ensuite, on fait le total de tous les lecteurs, on soustrait ce total de 100, et on obtient la réponse à la première question.

Merci pour la réponse!! Avec les cercles c'est beaucoup plus simple...
En fait, 6 lisent A, B, C ; 10 lisent A et B (16-6) et 9 lisent A et C (15-6).
Donc pour trouver A:
35-6-10-9= 10...

Et puis pareil pour les autres...Merci beaucoup! et bonne soirée Équipe de modération : Ce topic a été verrouillé et déplacé car il a déjà été traité et/ou ne figure pas dans le bon forum. Merci de consulter ce lien pour lire la suite.